論文読み - Attention Is All You Need

今回は “Attention Is All You Need”¹という論文を読みました。

導入

従来の系列データにおけるモデルには、Encoder と Decoder を含むような複雑な RNN や CNN が使われていたが、この論文では Attention という新しいメカニズムで Encoder と Decoder を繋ぐことで再帰や畳み込みを使わずに系列データを処理する Transformer というモデルを提案している。

再帰構造を持つモデル RNN は開発されてから長い間 LSTM や GRU などに代表される色々な工夫によって系列データの扱える長さを増やす努力をしてきたが、構造上どうしても長くなればなるほど情報の欠損が発生しやすくなる。
さらに、その逐次的なアーキテクチャゆえに、GPU などの並列計算資源を活用することが難しいという問題があった。

しかしこのモデルは、既存の再帰系モデルで問題となっていた系列の距離依存性の問題を解決し、また並列計算資源を活用することが容易であるという利点がある。

モデル

これまでの系列伝達モデルは入力系列を次元圧縮された固定長のベクトルに変換する Encoder と、そのベクトルを元に出力系列を生成する Decoder という 2 つの部分から構成されていたが、各ステップにおいて Auto-regressive(自己回帰) なモデルを使うことで、それまでに生成された主力を消費しながら次の系列データを予測する。

一方で今回提案される Transformer は、Encoder と Decoder の両方に Stacked Self-Attention と Position-wise という 2 つの技術を使用している。

Encoder

Encoder は $N = 6$ 個の同じレイヤーから構成されており、各レイヤーは 2 つのサブレイヤーから構成されている。

1. Multi-Head Self-Attention Mechanism
2. Position-wise Fully Connected Feed-Forward Networks

また、各サブレイヤーの周りには Residual Connection が採用されており、さらにその後に Layer Normalization が適用されている。

つまり、サブレイヤーの出力は $LayerNorm(x + Sublayer(x))$ という形で計算される。

NOTE

Residual Connection は、ResNetの構成部品として開発された 残差ブロック と呼ばれる構造である。
数式で表すと $H(x) = F(x) + x$ という構造を持つように、この時そのまま引き継がれる入力 $x$ を恒等写像と呼び、$F(x)$ を残差写像と呼ぶ。
出力にそのまま入力を足すことで、$F(x)$ が $x$ に対する微小な修正量として働き、制度劣化問題を解決することができる。

Decoder

Decoder は Encoder と同様に $N = 6$ 個の同じレイヤーから構成されており、各レイヤーは 3 つのサブレイヤーから構成されている。

1. Masked Multi-Head Self-Attention Mechanism
2. Multi-Head Self-Attention Mechanism
3. Position-wise Fully Connected Feed-Forward Networks

Encoder の出力に対して Multi-Head Self-Attention を適用することで、Decoder は Encoder が生成した情報を参照しながら次の系列データを生成することができる。

後述するが、Masked Multi-Head Self-Attention は、Decoder が未来の情報を参照しないようにするために、出力系列の各要素に対して未来の情報をマスクした上で Self-Attention を適用するものである。

Decoder も Encoder と同様に Residual Connection と Layer Normalization が各サブレイヤーに適用されている。

Attention

Attention は、入力系列の各要素に対して重み付けを行い、その重み付けされた情報を元に出力系列を生成するメカニズムである。

Scaled Dot-Product Attention

Scaled Dot-Product Attention は、Query $\boldsymbol{q}$ と Key $\boldsymbol{k}$ 、Value $\boldsymbol{v}$ という 3 つのベクトルを入力として受け取る。

$\boldsymbol{q}$ と $\boldsymbol{k}$ は同じ次元数 $d_k$ を持ち、$\boldsymbol{v}$ は次元数 $d_v$ を持つ。

この重み付けは、Query と Key の内積を取り、その結果を $\sqrt{d_k}$ で割ることでスケーリングを行い、Softmax 関数を適用することで計算される。

ただし、この Attention は複数の Query、Key、Value を同時に処理するため、行列$\boldsymbol{Q}$、$\boldsymbol{K}$、$\boldsymbol{V}$ を入力として受け取る。
（行列乗算にすると最適化された計算が可能である）

Attention 関数は以下のように表される。

$$\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$$

これは $\boldsymbol{q}_i$ と $K$ の内積を取り、保持している Key の横ベクトル一覧の中から Query に似た Key ベクトルを取り出し、その Key ベクトルに対応する Value ベクトルを取り出すという処理を全ての Query に対して行うものである。

Multi-Head Attention

Multi-Head Attention は、複数の Attention を同時に計算することで、異なる表現空間を学習することができる。

具体的には、$d_{model}$ 次元の Query、Key、Value を $h$ 個の異なる表現空間に射影し、それぞれの射影されたベクトルに対して Scaled Dot-Product Attention を適用する。

その後、それぞれの Attention の結果を連結し、最後に線形変換を行うことで、元の次元数に戻す。

$$\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \ldots, \text{head}_h)W^O \\ \text{where}\ \text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)$$

ここで、$W_i^Q \in \mathbb{R}^{d_{model} \times d_k}$、$W_i^K \in \mathbb{R}^{d_{model} \times d_k}$、$W_i^V \in \mathbb{R}^{d_{model} \times d_v}$、$W^O \in \mathbb{R}^{hd_v \times d_{model}}$ は重み行列である。

論文では $h = 8$ としている。

Position-wise Feed-Forward Networks

上記の各サブレイヤーの後には、Position-wise Feed-Forward Networks という全結合層が適用される。

Position-wise Feed-Forward Networks は、2 つの線形変換とそれらの間に ReLU 関数を適用することで構成される。

$$\text{FFN}(x) = ReLU(xW_1 + b_1)W_2 + b_2$$

レイヤーごとに異なる重み行列 $W_1$、$W_2$ が適用されるため、共有されないことに注意。

Embeddings and Softmax

Transformer は、入力系列と出力系列の各要素に対して Embedding を適用する。

これにより系列を $d_{model}$ 次元のベクトルの系列に変換し、Transformer の各レイヤーに入力する。

また、出力系列の各要素に対して線形変換を適用し、その後 Softmax 関数を適用することで、次の系列データの確率分布を計算する。

Positional Encoding

Transformer は並列計算による高速化をしたため、従来のモデルと違い再起や畳み込みによる位置情報の表現がない。
そのため、モデルが系列の順序(位置)情報を使えるようにするために Positional Encoding という手法を導入している。

三角関数を用いて、各位置に対して固有の位置情報を付与することで、系列データの順序情報をモデルに伝える。

$$\text{PE}_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d_{model}}}\right) \\ \text{PE}_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{model}}}\right)$$

ここで、$pos$ は位置情報、$i$ は次元数を表す。また、10000 はハイパーパラメータである。

NOTE
ここの 10000 は、位置が離れた時にエンコード後のベクトルがどれだけ異なるかを調整するためのハイパーパラメータである。
一般的にこのパラメータは大きくすればするほど位置情報の差異が大きくなり、小さくすればするほど位置情報の差異が小さくなる。²

この Positional Encoding を Embedding に加算することで、各位置に対して固有の位置情報を持つベクトルを生成して Encoder、Decoder に入力する。

正弦波や余弦波といった周期関数を用いることで位置表現の変換に使う値を -1 ~ 1 の範囲に抑えつつも、周期による重複が発生しないように周期を 10000 のような大きな値で広げている。
周期性により学習時以上の長さの系列データがきても位置情報をオーバーフローさせずに表現することができる。

このような設計により、ユニークなベクトル表現をうまいこと生成することができる。

学習

論文では英独の翻訳タスクとして WMT 2014 English-to-German という 450 万文のペアを含むデータセットを用いて、Transformer モデルを学習している。

また、英仏の翻訳タスクとして WMT 2014 English-to-French という 3600 万文のペアを含むデータセットを用いて、Transformer モデルを学習している。

このデータセットの文章は 37000 の共有語彙からなるバイトペアエンコーディング(BPE)を用いてエンコードされた。

各バッチ約 25000 トークンのペアで学習を行い、最適化手法には Adam を用いている ($β1 = 0.9$, $β2 = 0.98$, $ε = 10^{-9}$)。
学習率はステップ数に応じて変化するスケジューリングを用いており、$d_{model}^{-0.5} \times \min(\text{step\_num}^{-0.5}, \text{step\_num} \times \text{warmup\_steps}^{-1.5})$ という式で計算される。
（学習率を直線的に増加させた後、ステップ数の逆平方根に比例して減少。実験では $warmup\_steps = 4000$ としている）

過学習を防ぐために Dropout や Label Smoothing などの正則化手法を用いている。

NVIDIA P100 GPU 8 台を用いて 300000 ステップ (3.5 日間) 学習を行い、学習済みモデルを得ている。

評価

他モデルとの比較

英独の翻訳タスクにおいて、Transformer モデルは BLEU スコアで 28.4 を達成し、モデルアンサブル込みの最先端の結果³である 26.36 から 2 BLEU ポイントの改善を達成している。

また、英仏の翻訳タスクにおいても、Transformer モデルは BLEU スコアで 41.8 を達成し、モデルアンサブル込みの最先端の結果³である 41.29 から 0.6 BLEU ポイントの改善を達成している。

実験後にドロップ率やビーム幅などのハイパーパラメータを調整した。
これらの結果では既存のモデルを上回る結果を達成しているにも関わらずトレーニングコストは 1/4 未満だった。

自己アーキテクチャの比較

News Test 2013 というデータセットを用いて、英独の翻訳タスクにおいて、Transformer モデル自身のどのコンポーネントが重要であるかを調査している。

例えば Attention Head の数を増やした場合、KV の次元数を減らすなどの変更を加えて、計算量をなるべく保つようにしながら、モデルの性能を調査している。

論文表 3 より、以下の調査結果が得られている。

• Single Head ($h = 1$) では ($h = 16$)時の最高 BLEU スコアに対して 0.9 ポイント低い結果となったが、逆に $h = 32$ のようにヘッドが多すぎるとスコアが低下する。
• Attention Key の次元数は小さくすると品質が低下する。
• $d_{model}$ が大きいほど、FFN の次元数が大きいと品質が向上する。
• Dropout がある方が、ない場合よりも品質が向上する。
• 既存の Positional Encoding 手法³でも同じような結果が得られた。

汎用性

Transformer モデルは、翻訳以外のタスクで一般化できるかどうかを調査している。

英語の構造解析タスクに対して、Transformer モデルを適用した。
Wall Street Journal の Penn Treebank で 40,000 文の訓練データを用いて学習を行い、テストデータで評価を行った。
特にタスクに特化したモデルというわけでもなく、ほぼ翻訳モデルの基本モデルをそのまま使っているにも関わらず、一部例外を除いて既存研究よりも高い性能を達成することができた。

まとめ

• Transformer は、再帰や畳み込みを使わずに系列データを処理する新しいモデルである。
• 並列化をベースとしたアーキテクチャにより、既存のアーキテクチャよりも明らかに高速に学習ができ、また翻訳タスクにおいて最高性能を達成することができる。
• Attention という新しいメカニズムを使うことで、系列データの長距離依存性の問題を解決している。
• 画像、音声、動画など、テキスト以外のモダリティを持つデータにも適用できる可能性がある。
• 他のタスクにも汎用化できる将来性を秘めており、追加研究が期待される。

議論

Positional Encoding の必要性について

考察

Positional Encoding がなければ、 どんな入力系列も同じ内部状態を持つ ことになるため、単なる Bag-of-Words モデルと同じような振る舞いをしそう。

Positional Encoding は入力系列に位置に敏感な逐次的な依存性を注入させることで、Transformer モデルが系列データの順序情報を理解できるようにしている。

トークンが生成されると、入力は位置情報が変わることで生成前とは異なる内部状態を持つようになるが、もし Positional Encoding がない場合、トークンが生成され次に進んでも同じ内部状態を持つことになるために 系列情報の順序を理解できなくなる のではないか。

直接的な Positional Encoding の効果に関する研究を見つけることができなかったが、Decoder-Only Transformer モデルにおいて Positional Encoding を使わないという選択が有効であることを示し、Transformer 全体への課題として位置関係表現の改善が今後有望であると述べている論文を見つけた。

Positional Encoding の効果に関する研究

Positional Encoding が Decoder-Only Transformer モデルの課題である コンテキスト長の汎化 にどのように影響を与えるかを調査した論文⁴によると、Positional Encoding はコンテキスト長が長いほど性能が向上することが示されている。

Transformer では再帰的な構造をやめたために、 入出力が長くなるにつれて性能が低下する という問題は解決したものの、 小さいコンテキスト長で学習したモデルがそれ以上の大きな入力に対しては性能が低下する という新たな問題が発生している。

Positional Encoding はこの問題を解決するために導入されたが、その効果については議論が分かれおり、この論文では

• APE (Absolute Positional Encoding)
• RPE (Relative PE)
• ALiBi (Attention with Learned Biases)
• Rotary
• No PE (Positional Encoding を適用しない場合)

のような手法を比較し、以下画像のタスクを使い、デコーダーのみの Transformer モデルを使って、さまざまな Positional Encoding の効果を調査している。

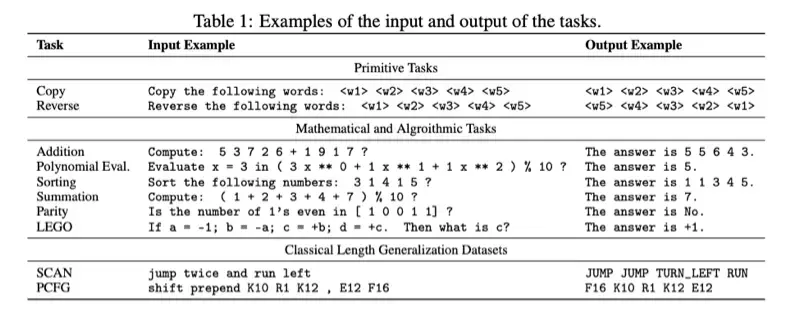
以下画像はそれぞれのタスクでの単純な精度による比較である。

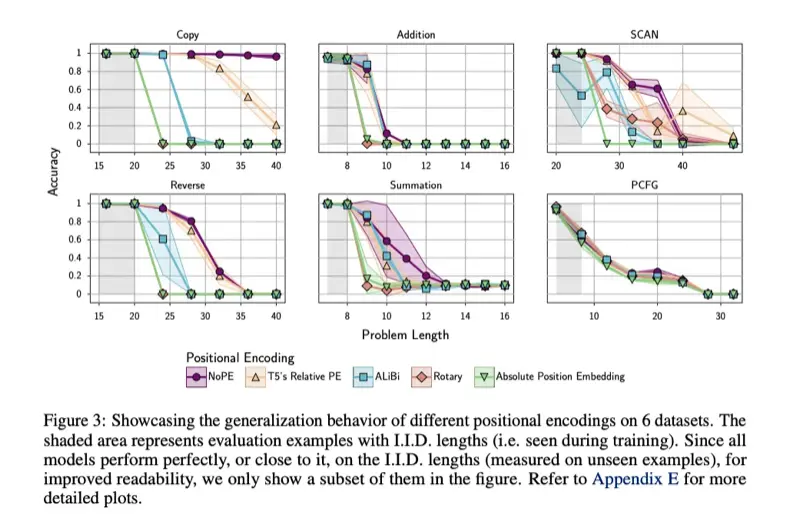
特に Copy と Reverse, Summation のタスクにおいて、NoPE が明らかに問題長に対する精度の低下が緩やかで、その他の Positional Encoding を採用したモデルよりも性能が高いことが示されている。

定量評価より NoPE は暗黙的に絶対位置と相対位置を両方学習することができていることがわかった。
（長いのでなぜそうなるのかは省略。⁴の 5.1 節 “NoPE can theoretically represent both absolute and relative PEs” を参照）

最後に、この論文では Positional Encoding が Transformer のコンテキスト長の汎化の課題をもたらしている一因である証拠であることを指摘しており、改善方法として除去または別の方法での位置関係表現が今後有望であると述べている。
また、特に Decoder-Only Transformer モデルにおいては、Positional Encoding を使わないという選択が有効であることが示された。

Footnotes

1. Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, Illia Polosukhin, “Attention Is All You Need”, 2017 ↩

2. Why is 10000 used as the denominator in Positional Encodings in the Transformer Model? ↩

3. Jonas Gehring, Michael Auli, David Grangier, Denis Yarats, Yann N. Dauphin., “Convolutional sequence to sequence learning.”, 2017 ↩ ↩² ↩³

4. Amirhossein Kazemnejad, Inkit Padhi, Karthikeyan Natesan Ramamurthy, Payel Das, Siva Reddy, “The Impact of Positional Encoding on Length Generalization in Transformers”, 2023 ↩ ↩²