← Back

論文読み - SayCanPay: Heuristic Planning with Large Language Models using Learnable Domain Knowledge

今回は “SayCanPay: Heuristic Planning with Large Language Models using Learnable Domain Knowledge”1という論文を読みました。

導入

LLM は近年の研究で プランニング のタスクにおいても有用であることが示されてきた。

しかし LLM におけるプランニングでは次のような問題がある。

  • 事前に学習された世界モデルと異なる環境であること
    • 実行可能でない行動を生成する
      • eg:「冷蔵庫が空いていないのにりんごを取り出そうとする」
      • SayCan2 はこの問題を解決するために、Pre-Trained な問い合わせ方法でその行動が実現可能かどうかの情報を外部から取得することでアフォーダンスを考慮している
    • 存在しないオブジェクトを参照する
      • eg:「部屋にない椅子に座ろうとする」
  • 最終的なゴールとの関連性が低い
    • 最終結果としての最適を選ぶことが難しい
    • 次の行動を貪欲に選択する
      • 計画が長くなり最終的なコスト効率が悪くなる

これらの理由から費用対効果や実現可能性などの観点では未だ十分な性能を発揮できていない。

一方、これまでプランニングでは、ドメイン知識と発見的探索を用いた発見的計画手法が使われ、ヒューリスティック探索による力で問題を解決してきた。
しかし、いろいろな問題(= 世界)への適応を考えた時、実世界環境のドメインファイルを入手することは困難であり、プランナーの使用は閉じた世界に制限されてしまう。

そこで本論文では、LLM が持つ世界知識とヒューリスティック探索を組み合わせる 新たな手法 SayCanPay を提案する。

図1: LLMプランナーの比較
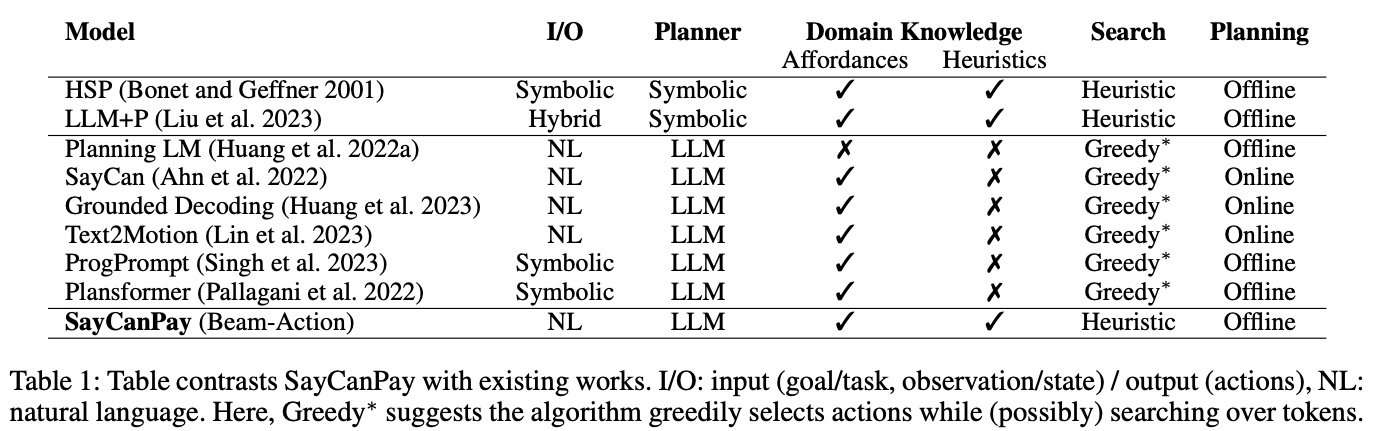
llm planner comparison

Q:なぜSayCanがオンラインプランニングなのに対してSayCanPayはオフラインプランニングなのか？

SayCan はオンラインプランニングを行うため、次の行動を考えるたびに問い合わせをし都度情報を取得する。つまりゴールとの長期的な関連性は考慮せず次の実行可能な行動を貪欲に選択することに焦点を当てており、近視眼的な性質がある。そもそも行動の計画生成と実行が各ステップで行われるため、状態追跡が単純で貪欲にならざるを得ないのである。

一方、SayCanPay はオフラインプランニングを採用しており、内部の環境の状態を保持しながら計画生成を行うことができる。そのため、全体を見た行動の探索を行うことができ、最終的なゴールとの関連性を考慮した計画を生成することができる。

手法

POMDPによる定式化

このプランニング問題は、近似的なプランニングに基づき、部分的観測可能マルコフ決定プロセス（POMDP）として定式化され、この POMDP は、タプル ⟨S,SG,b0,A,O,R,T⟩\langle S, S_G, b_0, A, O, R, T \rangle で定義される。

  • SS: 状態空間
  • SG⊆SS_G \subseteq S: 目標状態の集合
  • b0b_0: 初期信念状態
  • AA: 行動集合
  • OO: 観測の集合
  • R:O→RR: O \rightarrow \mathbb{R}: 観測関数
  • TT: ホライゾンの長さ

POMDP 自体は他と変わらなさそうなので、ここでは省略する。

ヒューリスティック検索プランニング

Heuristic Search Planning (HSP)3 を使って状態空間が非常に大きい世界を探索する。

Ht=(A×O)t−1H_t = (A \times O)^{t-1} をステップ tt でエージェントが持つ履歴、すなわち行動と観測のシーケンス {(o0,a1,o1,…,at−1,ot−1)}\{(o_0, a_1, o_1, \dots, a_{t-1}, o_{t-1})\} と定義する。

HSP では、コスト推定関数 fheur:Ht×SG→Rf_{heur}: H_t \times S_G \rightarrow \mathbb{R} を使用し、エージェントが行動を選択する際に探索プロセスを支援します。

例えばとして最も有望な次の行動を、過去に蓄積されたコスト faccf_{acc} と履歴 ht=(ht−1,at)h_t = (h_{t-1}, a_t) と目標 gg から推定されたコスト fheurf_{heur} に基づく線形結合によって選択するアルゴリズムが挙げられる。

コスト推定関数 fhtf_{ht} は以下の形で定義されます:

f(ht)=z1⋅facc(ht−1)+z2⋅fheur(ht,g)wherez1,z2∈{0,1}f(h_t) = z_1 \cdot f_{acc}(h_{t-1}) + z_2 \cdot f_{heur}(h_t, g) \\ \text{where} \quad z_1, z_2 \in \{0, 1\}

次の行動 ata_t は最小の f(ht)f(h_t) を持つものとして選択されます。特定のケースとして、z1=1z_1 = 1 と z2=1z_2 = 1 で A* アルゴリズム、z1=0z_1 = 0 と z2=1z_2 = 1 で Greedy Best-First Search (GBFS) アルゴリズムが得られます。

4 章は言語モデルのトークンレベルでの探索(ビームサーチに代表される尤度総積の最大化手法)について述べられているが、論文ではこの手法がメインではなく、アクションレベルでの探索に興味があるとしている。

SayCanPay推論

  1. Say: 各ステップ t において、LM が上位 m 個のアクション候補を確率 {p(ati∣ht−1,g)}i=1m\{p(a_t^i | h_{t-1}, g)\}_{i=1}^m とともに生成する。この生成には LLM におけるトークンレベルのビームサーチが用いられる。
  2. Can: 訓練されたドメイン固有モデルが前提条件評価を反映する形でこれらの候補アクションの実行可能性を評価する。
  3. Pay: 最後に、訓練されたドメイン固有の推定モデルによってペイオフを評価し、先ほど生成したアクション候補に重み付けを行う。

つまり三つの評価指標によって行動候補に推定コストによる優先順位をつけ、それを探索するということである。

図2: SayCanPayがBabyAI環境で次の行動をどのようにスコアリングするかのデモ
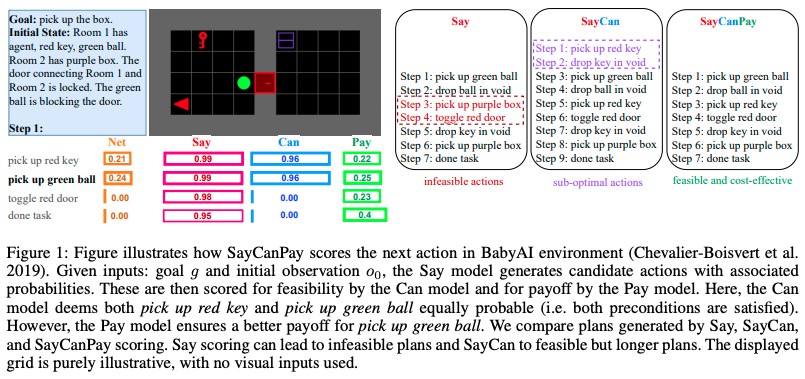
Demo of SayCanPay

図 2 では実行可能性(= Can)は赤の鍵を拾っても緑のボールを拾っても等確率であるが、ペイオフ(= Pay)は緑のボールを拾う方が良いペイオフであることを示している。
最終的に Say, Can, Pay のそれぞれのスコアをかけた値を図中の Net が示していて、この場合 pick up green ball が最も高いスコアを持つため、この行動が選択される。

図 2 右側で、同じ環境で Say モデル、SayCan モデル、SayCanPay モデルの出力を比較している。

Say モデルでは 実行不可能な計画 を導き出している。
SayCan モデルでは実行可能な計画だが、長い計画 を導き出している。
SayCanPay モデルでは 実行可能かつコストが低い計画 を導き出せている。

この後、貪欲とビームサーチのアルゴリズムについて解説が続くが、そのままなので省略する…

モデルの訓練

ドメインに特化したモデルを学習するために、N 個の Expert-Trajectories E={τ}i=1N\mathcal{E} = \{\tau\}_{i=1}^N を収集する。ここで τi={(o0,g,a1,a2,…,aT,r}\tau_i = \{(o_0, g, a_1, a_2, \dots, a_T, r\} であり、Expert であるためいずれも r=1r = 1 である。

Canモデルの訓練

Can モデルは、分類問題としてモデル化し InfoNCE 損失を最小化することで訓練される。

−1B∑i=1Blog⁡Mcan(ht−1i,gi,ati)∑a∈{ati,atˉ≠ti,a~i}Mcan(ht−1i,gi,a)- \frac{1}{B} \sum_{i=1}^{B} \log \frac{\mathcal{M}^{\text{can}}\left(h_{t-1}^i, g^i, a_t^i\right)}{\sum_{a \in \{a_t^i, a_{\bar{t} \neq t}^i, \tilde{a}^i\}} \mathcal{M}^{\text{can}}\left(h_{t-1}^i, g^i, a\right)}
  • BB: バッチサイズ
  • ata_t: Expert-Trajectory τi\tau_i からサンプルしたステップ tt でのアクション (Positive Action)
  • Mcan\mathcal{M}^{\text{can}}: Can モデル (実行可能性を評価するモデル)
  • atˉ≠tia_{\bar{t} \neq t}^i: Expert-Trajectory からサンプルしたステップ tt 以外でのアクション (Negative Action)
  • a~i\tilde{a}^i: Expert-Trajectory τi\tau_i 以外からサンプルしたアクション (Negative Action)

つまりその履歴で次に正しいアクションをするただ一つの Positive Action と、それ以外のアクションを Negative Action として、ロスを最小化すれば、履歴から正しいアクションを選択するモデルを学習できる。

McanM^{\text{can}} は確率出力層を持つ Uncased BERT Model として実装する。

入力は次のような形式である:
⟨Goal⟩{g}⟨History⟩{ht−1}⟨NXT⟩{at}\langle Goal \rangle \{g\} \langle History \rangle \{h_{t-1}\} \langle NXT \rangle \{a_t\}

  • ⟨∗⟩\langle * \rangle: Special Token

出力は行動の実行可能性を表す確率値である。

この学習方法は SayCan2 とは異なり、Temporal Difference Based Reinforcement Learning により学習される。

詳細な入出力例

Input ⟨Goal⟩\langle Goal \rangle pick up the purple box. ⟨InitialState⟩\langle Initial State \rangle Room 1 has yellow key, agent. Room 2 has purple box. The door connecting Room 1 and Room 2 is locked. ⟨Step1⟩\langle Step 1 \rangle pick up yellow key. ⟨NXT⟩\langle NXT \rangle toggle yellow door.
Output 1.0 // feasible

Input ⟨Goal⟩\langle Goal \rangle pick up the purple box. ⟨InitialState⟩\langle Initial State \rangle Room 1 has yellow key, agent. Room 2 has purple box. The door connecting Room 1 and Room 2 is locked. ⟨Step1⟩\langle Step 1 \rangle pick up yellow key. ⟨NXT⟩\langle NXT \rangle pick up purple box.
Output 0.0 // infeasible

Payモデルの訓練

一方、Pay モデルは、回帰問題としてモデル化し、MSE 損失を最小化することで訓練される。
Expert-Trajectories E\mathcal{E} を用いて各バッチを [g,ht−1,at,r]1:B[g, h_{t-1}, a_t, r]^{1:B} とするデータセットを作成する。

このとき、ゴールに近いほど割合が高いことを表現するために、割引定数 δ∈(0,1)\delta \in (0, 1) を導入し報酬を rt−1=δ,rt−2=δ2,…,r0=δTr_{t-1} = \delta, r_{t-2} = \delta^2, \dots, r_0 = \delta^T のように定める。もちろん rt=1r_t = 1 である。

MpayM^{\text{pay}} は [0,1][0,1] bounded な Regression レイヤーを持つ Uncased BERT Plus Model として実装する。

入力形式は Can モデルと同様であるが、出力は推定ペイオフ fheur(ht,g)=Mpay(g,ht−1,at)f_{heur}(h_t, g) = M^{\text{pay}}(g, h_{t-1}, a_t) である。

詳細な入出力例

Input ⟨Goal⟩\langle Goal \rangle pick up the purple box. ⟨InitialState⟩\langle Initial State \rangle Room 1 has yellow key, agent. Room 2 has purple box. The door connecting Room 1 and Room 2 is locked. ⟨Step1⟩\langle Step 1 \rangle pick up yellow key. ⟨Step2⟩\langle Step 2 \rangle toggle yellow door. ⟨Step3⟩\langle Step 3 \rangle drop key in void. ⟨Step4⟩\langle Step 4 \rangle pick up blue box. ⟨NXT⟩\langle NXT \rangle done picking up.
Output 1.0 // end of plan

Input ⟨Goal⟩\langle Goal \rangle pick up the purple box. ⟨InitialState⟩\langle Initial State \rangle Room 1 has yellow key, agent. Room 2 has purple box. The door connecting Room 1 and Room 2 is locked. ⟨Step1⟩\langle Step 1 \rangle pick up yellow key. ⟨Step2⟩\langle Step 2 \rangle toggle yellow door. ⟨Step3⟩\langle Step 3 \rangle drop key in void. ⟨Step4⟩\langle Step 4 \rangle pick up blue box. ⟨NXT⟩\langle NXT \rangle pick up green box.
Output 0.6 // δ · r

Input ⟨Goal⟩\langle Goal \rangle pick up the purple box. ⟨InitialState⟩\langle Initial State \rangle Room 1 has yellow key, agent. Room 2 has purple box. The door connecting Room 1 and Room 2 is locked. ⟨Step1⟩\langle Step 1 \rangle pick up yellow key. ⟨Step2⟩\langle Step 2 \rangle toggle yellow door. ⟨Step3⟩\langle Step 3 \rangle drop key in void. ⟨Step4⟩\langle Step 4 \rangle pick up blue box. ⟨NXT⟩\langle NXT \rangle pick up green box.
Output 0 // very low payoff

実験

Sayモデル

  • LLaMA (13b) をファインチューニングした Vicuna モデル Decoder Only
  • Flan-T5 (11b) Encoder-Decoder

これらのモデルを FT なしでそのまま推論に使った。
アクションは自然言語で出力されるため認識できない単語・不正確な構文を含む可能性がある。そこで最小編集距離を用いて生成されたアクションに最も近いアクションへマッピングすることで正規化を行った。

実験環境

評価項目

  • 成功率
  • 費用対効果
  • 分布外(ODD)汎化

データ

RavensとVirtual Homeには800、BabytAIには400のExpert-Trajectoriesが用意されている。

結果

表3 は環境ごと・モデルごとに様々なモデルの組み合わせで100プラン実行した中での制約内での成功数が示されている。これは単純に成功率を示すものである。
(その中でもVirtual Homeは自由度が高いので手動で成功かどうかの判断を行った)

表4 はExpert-Trajectories と同じプラン長のプラン生成が100プラン中にどれだけ含まれているかを示している。これは最良をどれだけ探索できているかを示す費用対効果の指標である。

表5 では3,4と同じ実験を訓練とテストを異なる環境間で分割して行った結果を示している。これはモデルがどれだけ他の環境に汎化できるかを示す指標である。

成功率からみるスコアパフォーマンス的にはおおかた Say < SayCan <= SayCanPay のような関係性となっており、しばしば SayCanPay が SayCanを上回ることができている。
論文ではこれについてビームサーチによる多様性の確保が結果的に長期的な関連性（累積コスト）に基づいて行動を選択できているという点で、部分的に制約内での成功率が高くなったとしている。

費用対効果を見ると、ほとんどのBeam-Action, Greedy-Actionにおいて SayCanPay がSayやSayCanモデルを上回り、性能改善していることがわかる。

汎化性能面では性能が向上した環境と逆にSay > SayCan > SayCanPay のような性能低下がみれれるケースがあった。このことから、今回学習されたドメインモデル(=Can, Pay)が特定の環境に過剰適合してしまっている可能性があるとしている。 $7.5参照

モデルアーキテクチャ（Dec Only/Enc-Dec）については、一貫した性能向上が見られないが、スコアに差は現れどちらかが優位であることは判明したので今後の研究でLLMのアーキテクチャがどんなドメイン・形式のプランニングの問題に適しているかを検証する必要があるとしている。

Ablation Study

  • ビーム幅
    • 図3 ではビーム幅に対する性能の変化を示している。基本的にビームサーチの性質が露呈しており、ビーム幅が大きいほど全体的には性能が向上しているが、ビーム幅が大きくなると逆に多様性を確保しすぎて良い行動を見逃す結果となることがある。
  • Say Model
    • そもそもSayモデルが環境から次の行動を正しく提案できないことが、プランニング失敗のボトルネックになる可能性がある
    • Sayモデルを完全に正しく提案するよう修正したPerfect-Sayモデルを導入し、同様の実験を行った 表7
    • 表7 ではLLMのSayモデルに対しPerfect-Sayモデルが1.5~2倍の性能向上を示していおり、かなり成功率が向上していることがわかる
    • そのため、CanやPay以前にSayモデルの改良が必要であることが示唆された。

まとめ

従来の計画フレームワークにLLMの知識世界や生成能力を組み合わせて、実現可能性を担保しつつ費用対効果が高い計画を生成する手法の有効性を示した。
この手法によりよりロングホライズンな良い計画を生成できる手法が確立され、依然として課題はあるがLLMにおけるプランニングにおいて大きな進歩があることが示せた。

一方で

  • Expert-Trajectories が必要な点
  • OOD環境への適応性の限界

これらはモデルの大きさ、報酬設計へのLLM活用によって訓練を緩和し汎化を完全できる可能性があるとしている。

Footnotes

  1. Rishi Hazra, Pedro Zuidberg Dos Martires, Luc De Raedt, “SayCanPay: Heuristic Planning with Large Language Models using Learnable Domain Knowledge”, 2024 ↩

  2. Michael Ahn, Anthony Brohan, Noah Brown, et al. “Do As I Can, Not As I Say: Grounding Language in Robotic Affordances”, 2022 ↩ ↩2

  3. Bonet, Blai, and Héctor Geffner. “Planning as heuristic search.” Artificial Intelligence 129.1-2 (2001): 5-33. ↩

Copy URL
Source
Share X
← 2024年夏休みの振り返り
Home Works Timeline Blogs Slides