論文読み - Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference

今回は “Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference”¹という論文を読みました。

導入

近年の DL ベースのモデルは膨大な計算コストがかかることから、エッジデバイスやモバイルデバイスでの実行が難しいという問題があり、これを解決するために既存のモデルを新たな手法により量子化することを提案している。

近年のモバイルプラットフォーム(== スマートフォン, AR/VR, ドローンなど)での DL モデルでは、モデルサイズと推論時間を削減することによって実行を可能にしその分野での研究が盛んであるが、実際にハードウェアに対して検証しているわけではなく、あまり有効ではない高速化（ビットシフトやバイナリネットワークなど）が多い。
実際に比べるべくは精度とハードウェア上での推論速度のトレードオフである。

Quantization Scheme

論文では新たな量子化手法として以下の方法を提案している。

$$r = S(q - Z)$$

• $q$ : 量子化された値 (integer)
• $Z$ : 量子化された値の中心 (offset) の値 (integer)
• $S$ : 量子化された値のスケールの値 (float)
• $r$ : 量子化された値の実数値 (float)

$B$-bit 量子化に対して、$q$は B-bit の符号付き整数で表現される。

この時、パラメータとなるのは定数$Z$と$S$である。

これを行列演算に適用することを考える。

量子化された$N \times N$行列$r_1, r_2$に対して、$r_3 = r_1 \cdot r_2$を計算するとする。

行列$r_{\alpha}$の要素$r_{\alpha}^{(i, j)}$は以下のように表現される。

$$r_{\alpha}^{(i, j)} = S_{\alpha} (q_{\alpha}^{(i, j)} - Z_{\alpha})$$

そして行列積の結果$r_{3}^{(i, j)}$は以下のように表現される。

$$r_{3}^{(i, j)} = \sum_{k=1}^{N} r_{1}^{(i, k)} \cdot r_{2}^{(k, j)}$$

これを用いて、行列演算を$q_{\alpha}$に対して表現すると以下のようになる。

$$\begin{aligned} S_{3} (q_{3}^{(i, j)} - Z_{3}) &= \sum_{k=1}^{N} S_{1} (q_{1}^{(i, k)} - Z_{1}) \cdot S_{2} (q_{2}^{(k, j)} - Z_{2}) \\ S_{3} (q_{3}^{(i, j)} - Z_{3}) &= S_{1} S_{2} \sum_{k=1}^{N} (q_{1}^{(i, k)} - Z_{1}) \cdot (q_{2}^{(k, j)} - Z_{2}) \\ q_{3}^{(i, j)} - Z_{3} &= \frac{S_{1} S_{2}}{S_{3}} \sum_{k=1}^{N} (q_{1}^{(i, k)} - Z_{1}) \cdot (q_{2}^{(k, j)} - Z_{2}) \\ q_{3}^{(i, j)} &= Z_{3} + M \sum_{k=1}^{N} (q_{1}^{(i, k)} - Z_{1}) \cdot (q_{2}^{(k, j)} - Z_{2}) \end{aligned}$$

この時、$M = \frac{S_{1} S_{2}}{S_{3}}$で、この式において唯一の非負整数パラメータである。

求めた数式より、量子化結果は$Z_{3}$と$M$に依存し、これはどちらも定数であるため、オフライン（not 学習時）で計算することができる。

しかし、$M$が float ゆえに結局目的の整数演算のみでの推論は達成できない。
論文では、経験的に$M$が$[0, 1)$の範囲に収まることから、次のように$M$を表現することを提案している。

$$M = 2^{-n} M_0$$

$M_0$は$[0.5, 1)$の範囲に収まるように制約をかけ、その中でハードウェアの制約に適した$n$を使うことで固定小数点乗数を用いた整数演算のみでの推論を実現する。

実際にどれくらいの計算量で量子化が可能かどうかを考えると、$q_3^{{(i, j)}}$を展開して因数分解したときに

$$\begin{aligned} q_3^{{(i, j)}} &= Z_3 + M \sum_{k=1}^{N} (q_1^{{(i, k)}} - Z_1) \cdot (q_2^{{(k, j)}} - Z_2) \\ &= Z_3 + M \left( N Z_1 Z_2 - Z_1 \sum_{k=1}^{N} q_2^{{(k, j)}} - Z_2 \sum_{k=1}^{N} q_1^{{(i, k)}} + \sum_{k=1}^{N} q_1^{{(i, k)}} q_2^{{(k, j)}} \right) \end{aligned}$$

となり、支配的な部分の計算量はせいぜい$O(N^3)$であることがわかる。

一つのパーセプトロンの値を計算するのに必要なデータ量を考える。
論文図 1.1 (a)のように、入力と重みはそれぞれ uint8 で量子化されているものである時、$y = \sum_{i=1}^{N} x_i w_i$を計算することを考えると uint8^2 の和なので、uint32 として y の値を持つことができる。
その時、バイアスは y にそのまま加算されるため同じ次元である uint32 で量子化された値を持つこととなるが、モデルサイズに対してバイアスがそこまで大きな割合を占めておらず、バイアスは重みに比べ全体に作用するために精度が下がりやすいため、uint32 で持つのだと論文では述べられている。

そして output は input と同じ次元でないといけないため uint32 出力を uint8 にダウンキャストしてから活性化関数に通して output を得る。

Training

一般的な量子化のアプローチでは、表現空間の大きいパラメータで学習された重みを、学習後に小さい表現空間に量子化するというものだった。
論文ではPost-training quantizationと称されているこちらのアプローチは、大規模モデルでは機能するが小規模モデルでは精度が著しく低下することが知られている。
当たり前だが、解像度が等しくなるように量子化されるため、もし近い値が偏って分布していた場合にそれが量子化後に同じ値として丸められてしまうことがあり、小さなモデルであればあるほどその影響が大きくなるのである。

そのため、論文ではうまく学習時に重みを量子化前提で調整させることを提唱している。
実際には、学習時には重みを float32 で保持し、Backpropagation もそのまま行うが、モデルが forward(推論)する際の全結合層のアウトプットが活性化関数を通った後などのタイミングで実際の値ではなく量子化された値を扱うことで擬似的に学習時に量子化されることを想定した学習を行う。

この実際は勾配更新などは float32 で行われているが、出力を量子化された値として学習するやり方をFake quantizationと呼ぶ。

$$\begin{aligned} \text{clamp}(r; a, b) &:= \min (\max (r, a), b) \\ s(a, b, n) &:= \frac{b - a}{n - 1} \\ q(r; a, b, n) &:= \left\lfloor \frac{\text{clamp}(r; a, b) - a}{s(a, b, n)} \right\rceil s(a, b, n) + a \end{aligned}$$

式を見ればわかるように実際は float32 の値だが、uint8 の値のスケールで丸める操作をしている。

NOTE> $\lfloor x \rceil$は$x$を最も近い整数に丸める関数である。

モデルによっては Batch Normalization がレイヤーに含まれている場合があるが、Fake quantization を適用するには Batch Normalization によってスケールされた後の重みを量子化する必要があるため工夫が必要である。論文式(14)のように EMA(折りたたみ結果の指数移動平均)を用いて Batch Normalization のスケールを推定し、それに応じた量子化を行う。

理解し辛いので図を用意した。

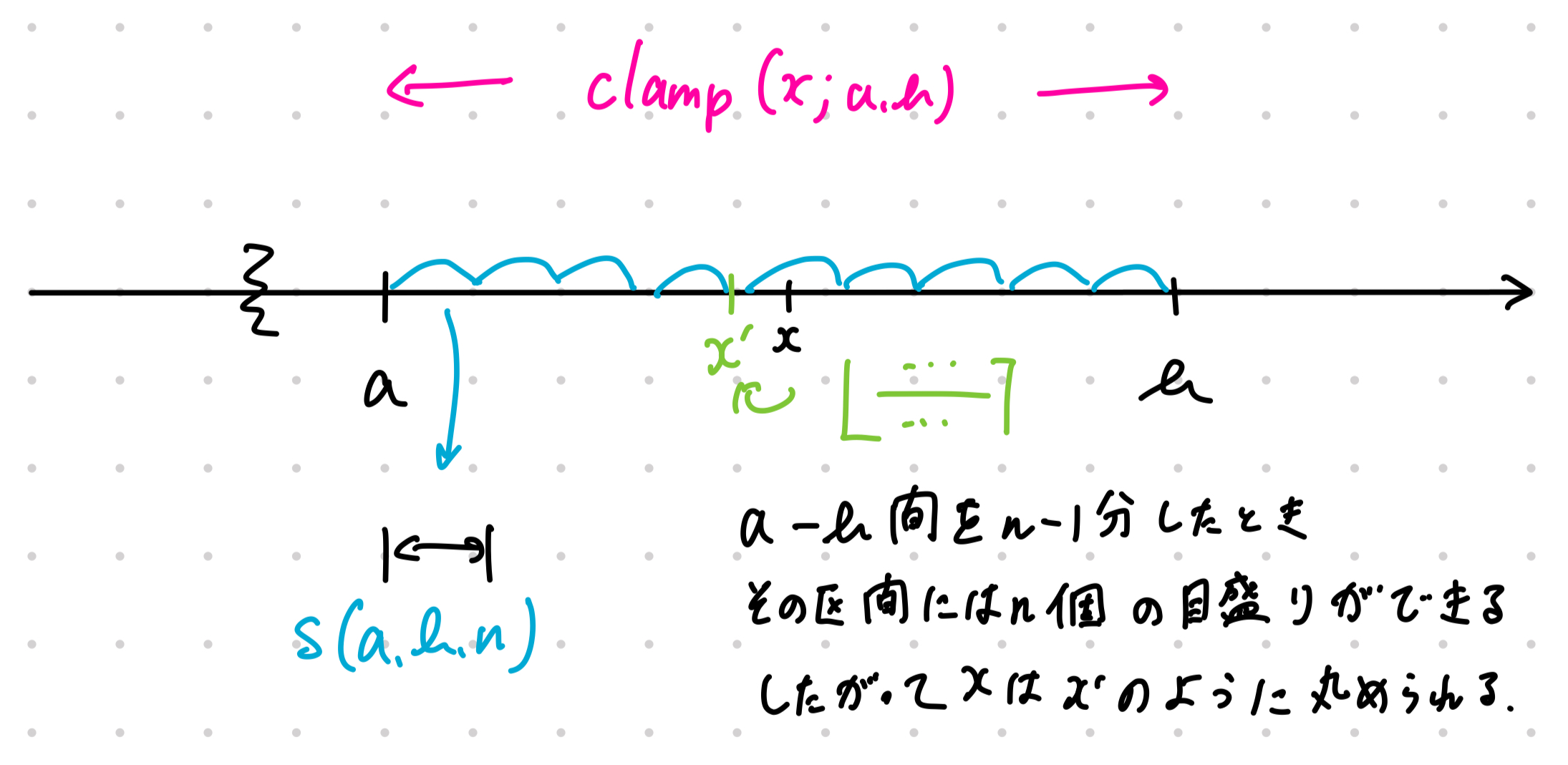
10 進整数の n 桁未満を切り捨てするときの

int x = 54321;
int y = x / 100 * 100;
cout << y << endl; // 54300;

のようなイメージで、float32 の値を uint8 の値に丸める操作をしている。

Experiments

大規模モデルにおける量子化

ResNet と Inception-v3 の 2 つのモデルを用いて、通常の学習と量子化学習をした後に量子化されたモデルを評価した。

ResNet を使ってさまざまなレイヤーの深さで学習した結果、Integer-quantized なモデルは Float-point モデルに比べて最大でも 2%程度の精度低下に抑えられている。

また、従来手法と比較したときに精度とモデルサイズのトレードオフをうまく調整できていることがわかり、また単純には比較できないが実行速度改善ができた。

次に Inception-v3 を使って、活性化量子化の精度を調べた。

1 ビット減らした 7bits の量子化でも、8bits と遜色ない性能が出ることがわかり、さらに精度は ReLU よりも ReLU6 の方が 1bit 減らした時の精度劣化が少ないことがわかった。

ちなみに、ReLU6 は ReLU の出力を$[0, 6]$にクリップしたもので、ReLU より小さなチャネルに縮まった状態で学習されるため、量子化された時に精度が落ちにくいようだ。

MobileNetとの比較

すでに ImageNet の分類タスクをエッジデバイスで行うために推論コストと精度のトレードオフの最先端の成果を出している MobileNet と、それを本手法で量子化したモデルを比較した。

論文図 1.1(c),4.1,4.2 にて、各チップで MobileNet のモデル(Float)に対して、今回の量子化モデル(8-bit)と本家 MobileNet と同等の精度を出すのにかかる推論コスト(=推論時間)を比較している。

試したデバイスは

• Snapdragon 835 LITTLE
• Snapdragon 835 BIG
• Snapdragon 821

で、それぞれのデバイスで MobileNet のモデルに対して、本手法で量子化したモデルが同等の精度を出すのにかかる推論コストがどれくらいかを比較している。
835 LITTLE では推論レイテンシが大体半分程度に削減できていることがわかった。（論文では対数スケールでレイテンシが表現されているので注意）
さらに、同じ推論時間で出せる精度という軸で見ると、10%程度の精度向上が見られた。
一方で 821 はそもそものチップが浮動小数点演算がより最適化されているため、それほど整数演算ベースに量子化したモデルが有利にならなかった。

COCO という物体検知評価のデータセットを使った比較では、論文図 4.4 のように実行時間を最大 50%程度量子化により削減できており、チップの性能が良いことが量子化の効果をより引き出すことができることがわかった。

Face Detection のタスクでも、MobileNet のモデルに対して本手法で量子化したモデルが同等の精度を出すのにかかる推論コストがどれくらいかを比較している。

結果約 2%の精度低下と引き換えに 2 倍の推論速度向上が見られた。
さらに使うスレッド数を増やした時にうまく速度も向上したことからマルチスレッドに対しても有効であることがわかった。
（ただし元モデルの速度が比較されていないのは気になる）

• Precision
• Recall
• DM

パラメータ比較

量子化の重みと活性化それぞれの bit 数を変化させて精度低下を調べたところ、重みが活性化よりも精度低下に敏感であること、7,8 ビットくらいであればそこまで性能低下を気にせず元モデルと同等の精度を出せること、総 bit 数が同じであれば重みと活性化の bit 数を等しくするのが良いことがわかった。

まとめ

量子化をシミュレートして学習させる手法により、精度低下を最小限に抑えつつ、推論速度を向上させることができることがわかった。
ARM NEON などの整数演算ベースのハードウェアに対してとても有効であることがわかった。
GPU の力をそこまで使えないエッジデバイスにおいて、モバイルデバイスでの推論を実現するためには、このような量子化手法が有効であることがわかった。

面白そうだと思った論文

検索などで見つけた記事²や Twitter での情報を参考に、面白そうだと思った論文をまとめた

The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits

Microsoft の中国チームが提案した 1-bit(1.58bit)の LLM 量子化手法についての論文。
重みを {-1, 0, 1} の 3 値で表現することで、重みが log2(3) = 1.58 ビットで表現でき、同じモデルサイズ（つまり圧縮した分だけモデルを大きくできる）で FP16 や BF16 で学習された Transformer モデルと同等の精度を出すことができるというもの。
{-1, 0, 1} の演算は全てビット演算のみで行われるため、エネルギー効率が非常に高いらしい。(2024/02/27)

Exploiting LLM Quantization

量子化された時だけ悪意のある振る舞いをする LLM を作って HF のリーダーボードなどに公開し、ユーザーがダウンロードしてはじめて量子化した時に広告や有害な思想などの出力をさせることができ、悪用の危険性があるという指摘。(2024/05/28)

Reward Design with Language Models

人間が強化学習の報酬を設計するのには多大な労力がかかる。LLM に代理評価関数としてプロンプトに記述された期待している行動からの評価を行わせることで、人間が報酬設計をする手間を省くことができるというもの。(2023/02/27)

Guiding Pretraining in Reinforcement Learning with Large Language Models

強化学習はランダム探索によってこれまで学習されてきたが明らかにサンプル効率が悪い。LLM を使ってタスクを分解させてうまくガイドすることでサンプル効率を向上させることができるというもの。(2023/02/13)

Grounding Large Language Models in Interactive Environments with Online Reinforcement Learning

LLM が常識的な判断力を備えていることから、行動決定が可能であるといえ、確率方策モデルとして使えるのではないかという仮説を検証している。
FLAN-T5 を確率方策モデルに使って PPO を行ってサンプル効率が向上したらしい。(2023/05/12)

Footnotes

1. Shibani Santurkar, Dimitris Tsipras, Brandon Tran, Andrew Ilyas, Logan Engstrom, Aleksander Madry, “Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference”, 2018 ↩

2. https://horomary.hatenablog.com/entry/2023/11/24/225302 ↩